Skip to main content

Sinuoidal Functions II

We will continue with sinusoidal type functions for the examples we will present, but now from R2→R\mathbb{R}^2\to\mathbb{R}. For the examples, we will use the following libraries,

# Libraries
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

and we're going to have to have Ω⊂R2\Omega\sub\mathbb{R^2} is compact (closed and bounded).

Implementation in more dimensions, now for sin⁡(x+y)\sin(x+y)​

Let Ω=[−2π,2π]×[−2π,2π].\Omega=[-2\pi, 2\pi]\times [-2\pi, 2\pi]. The idea is to approximate a neural network Φ:Ω→R\Phi:\Omega\to\mathbb{R} to the continuous function f:Ω→Rf: \Omega\to\mathbb{R}, f(x,y)=sin⁡(x,y)f(x,y)=\sin(x,y).

To calculate the points of the domain and the function in the domain,

# Omega domain
num_points = 256
omega_x = np.linspace(-2*np.pi, 2*np.pi, num_points, dtype="float64")
omega_y = np.linspace(-2*np.pi, 2*np.pi, num_points, dtype="float64")
omega_x, omega_y = np.meshgrid(omega_x, omega_y) 
omega = np.stack([omega_x.ravel(), omega_y.ravel()], axis=1)
f_omega = np.sin(omega[:,0]+ omega[:,1]) # function sin(x+y) "implementation"

omega_x_tf = tf.convert_to_tensor(omega[:,0][:, np.newaxis])
omega_y_tf = tf.convert_to_tensor(omega[:,1][:, np.newaxis])
f_omega_tf = tf.convert_to_tensor(f_omega[:, np.newaxis])

Construction of a neural network of Rn→R\mathbb{R}^n\to\mathbb{R}

# Single hidden Layer Neural Network Phi wit M=400 hidden units
M = 400
weight_x = tf.Variable(tf.random.normal([1,M], dtype=tf.float64))
weight_y = tf.Variable(tf.random.normal([1,M], dtype=tf.float64))
beta = tf.Variable(tf.random.normal([M], dtype=tf.float64))
alpha = tf.Variable(tf.random.normal([M,1], dtype=tf.float64))

@tf.function
def Phi(x, y):
    return tf.matmul(
        tf.keras.activations.tanh(
            tf.add(
                tf.add(tf.matmul(x, weight_x), tf.matmul(y, weight_y)),
                beta
            )
        ),
        alpha
    )

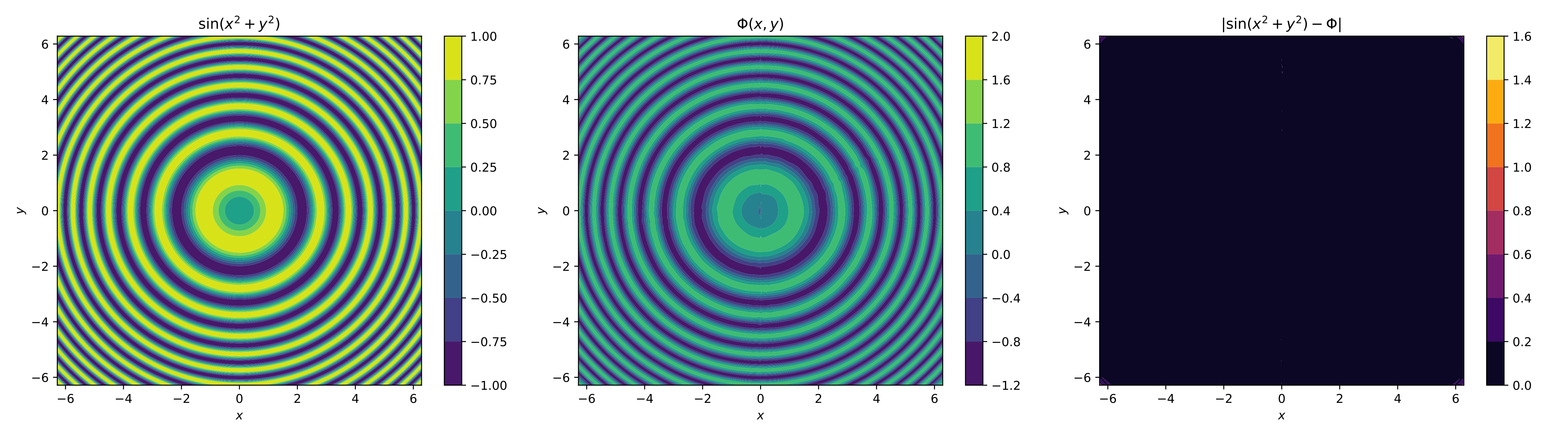
For the visual element, we only plot the contours of the original function, the neural network and its absolute error,

# training by gradient descent
learning_rate = 0.1
training_epochs = 4000

optimizer = tf.keras.optimizers.Adam(learning_rate)
mse = tf.keras.losses.MeanSquaredError()

for epoch in range(training_epochs):
    with tf.GradientTape() as tape:
        loss = mse(Phi(omega_x_tf, omega_y_tf), f_omega_tf)
    gradients = tape.gradient(loss, [weight_x, weight_y, beta, alpha])
    optimizer.apply_gradients(zip(gradients, [weight_x, weight_y, beta, alpha]))

For the visual, we only plot the contours of the original function, the neural network, and the absolute error,

# Graphic
f_omega = f_omega_tf.numpy().reshape((num_points, num_points))
f_omega_nn = Phi(omega_x_tf, omega_y_tf).numpy().reshape((num_points, num_points))

fig, axs = plt.subplots(1, 3, figsize=(18, 5))

cf1 = axs[0].contourf(omega_x, omega_y, f_omega, cmap='viridis')
axs[0].set_title("$\\sin(x^2+y^2)$")
plt.colorbar(cf1, ax=axs[0])

cf2 = axs[1].contourf(omega_x, omega_y, f_omega_nn, cmap='viridis')
axs[1].set_title("$\\Phi(x,y)$")
plt.colorbar(cf2, ax=axs[1])

cf3 = axs[2].contourf(omega_x, omega_y, np.abs(f_omega - f_omega_nn), cmap='inferno')
axs[2].set_title("$|\\sin(x^2+y^2) - \\Phi(x,y)|$")
plt.colorbar(cf3, ax=axs[2])

for ax in axs:
    ax.set_xlabel("$x$")
    ax.set_ylabel("$y$")

plt.tight_layout()
plt.show()

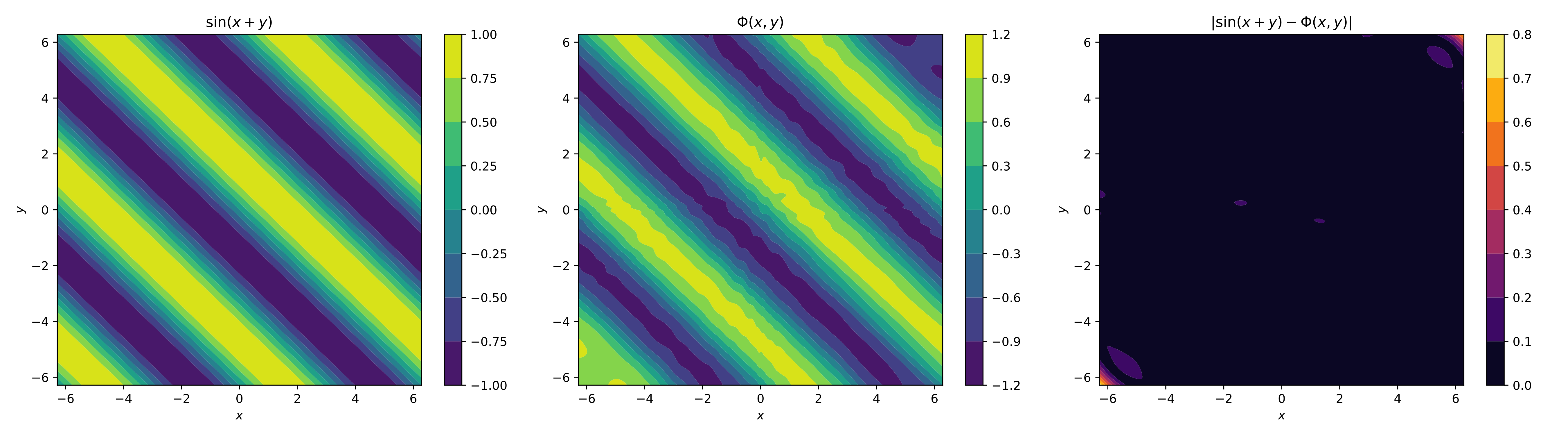
function approximation sin(x+y)

Another style of implementation, now for sin⁡(x2+y2)\sin(x^2+y^2)​

As you can see, when we added a dimension, it became a bit more difficult to implement the functions, even though we only used a single layer. For this, there are equivalent ways to implement neural networks with multiple layers and outputs.

function approximation sin(x+y)